Quantum Cryptography
1. what is Quantum Cryptography?

Quantum Cryptography is a cutting-edge field that uses the principles of quantum mechanics to secure communication and protect sensitive data from eavesdropping. Traditional cryptography relies on mathematical algorithms to secure data, but the security of these methods can be compromised with the power of advanced computing, particularly quantum computers. Quantum cryptography, on the other hand, uses the unique properties of quantum mechanics, such as superposition, entanglement, and the no-cloning theorem, to create fundamentally secure communication channels that cannot be easily intercepted or decrypted by unauthorized parties.
One of the most well-known protocols in quantum cryptography is Quantum Key Distribution (QKD). QKD allows two parties to generate a shared, secret key over a potentially insecure communication channel, with the guarantee that any attempt by an eavesdropper to intercept the key will be detected. This is because, according to the laws of quantum mechanics, measuring a quantum system disturbs its state. In practice, QKD uses quantum bits (qubits) transmitted in a superposition of states, and any attempt by an eavesdropper to measure the qubits will introduce detectable errors into the communication. The most popular QKD protocol is BB84, introduced by Charles Bennett and Gilles Brassard in 1984, which ensures that both parties can securely share a key, even in the presence of an adversary.
Quantum cryptography’s primary advantage over traditional cryptographic systems lies in its security based on the laws of physics rather than mathematical assumptions. For example, while the security of classical encryption methods, such as RSA, depends on the difficulty of factoring large numbers, a sufficiently powerful quantum computer could break these encryption schemes in polynomial time using Shor’s algorithm. However, quantum encryption is inherently secure against such attacks, as the principles of quantum mechanics prevent any undetected eavesdropping. Quantum cryptography is also being explored for quantum-safe cryptography methods, which aim to provide cryptographic security in a world where quantum computers are capable of breaking classical systems.
2.Quantum Key Distribution (QKD)
Quantum Key Distribution (QKD)is a technique in quantum cryptography that enables two parties to securely share a secret key over an insecure communication channel. The primary advantage of QKD over traditional cryptographic methods lies in its ability to detect eavesdropping and ensure the security of the key exchange based on the fundamental laws of quantum mechanics, rather than relying on the computational difficulty of mathematical problems. This makes QKD highly resistant to potential threats posed by future quantum computers, which could break classical encryption algorithms like RSA.
The basic principle behind QKD is the no-cloning theorem of quantum mechanics, which states that an arbitrary unknown quantum state cannot be copied exactly. This property prevents an eavesdropper from intercepting and copying the quantum key without disturbing the system. Additionally, quantum measurement disturbs the state of a quantum system, meaning that if an eavesdropper tries to observe the quantum key while it's being transmitted, they will inevitably introduce errors in the system, alerting the communicating parties to the presence of an intruder.
While QKD provides theoretically unbreakable security, practical implementation faces challenges such as the loss of quantum signals over long distances, which leads to the need for advanced technologies like quantum repeaters and satellite-based QKD. Quantum repeaters, which enable the transmission of quantum information over long distances by overcoming signal loss, are still in the developmental stage. However, advancements like the Micius satellite, which successfully demonstrated QKD over long distances, have shown the potential for global-scale secure communication networks using QKD.
.webp)
3. Post-Quantum Cryptography
Post-Quantum Cryptography
refers to the field of cryptography that aims to develop secure algorithms and systems that are resistant to attacks by quantum computers. Quantum computers, with their ability to efficiently solve problems like factoring large numbers (via Shor’s algorithm) and solving discrete logarithms (via the same algorithm), pose a significant threat to traditional cryptographic systems such as RSA and ECC (Elliptic Curve Cryptography). These cryptographic schemes form the backbone of much of today’s internet security, including data encryption, digital signatures, and key exchanges. As quantum computing advances, the need for new cryptographic systems that are resistant to quantum attacks becomes increasingly urgent. PQC focuses on creating cryptographic algorithms that are secure against both classical and quantum computational threats, ensuring the continued protection of sensitive data even in a future dominated by quantum computers.
The main goal of Post-Quantum Cryptography is to develop new public-key cryptographic algorithms that can withstand quantum attacks while remaining efficient and feasible to implement on current classical hardware. The National Institute of Standards and Technology (NIST) initiated a process to standardize post-quantum cryptographic algorithms and has been evaluating candidate algorithms for various cryptographic primitives, including encryption schemes, key exchange protocols, and digital signatures. These algorithms generally fall into different categories, such as lattice-based cryptography, hash-based cryptography, code-based cryptography, multivariate polynomial cryptography, and isogeny-based cryptography, each offering different advantages in terms of security and efficiency. Lattice-based cryptography, for example, is one of the most promising approaches, offering strong security assumptions and efficient performance in both key exchange and encryption tasks.
A critical aspect of Post-Quantum Cryptography is ensuring that the new algorithms are practical for implementation and do not significantly degrade performance in real-world applications. For instance, a key challenge is the increased key sizes and larger computational overheads associated with many post-quantum algorithms compared to classical cryptography. These factors could impact their deployment in existing systems, such as securing internet traffic, cloud storage, and digital certificates. Moreover, since most current systems rely on RSA or ECC, transitioning to quantum-resistant algorithms involves not only technical challenges but also widespread adoption and infrastructure updates. The timeline for this transition is critical, as quantum computers capable of breaking classical encryption schemes may not be far off. The development and standardization of post-quantum cryptography will ensure that once quantum computers become a reality, we will have secure cryptographic methods in place, safeguarding digital communications, financial transactions, and privacy in a quantum-enabled world.

4.Shor’s Algorithm
Shor’s Algorithm
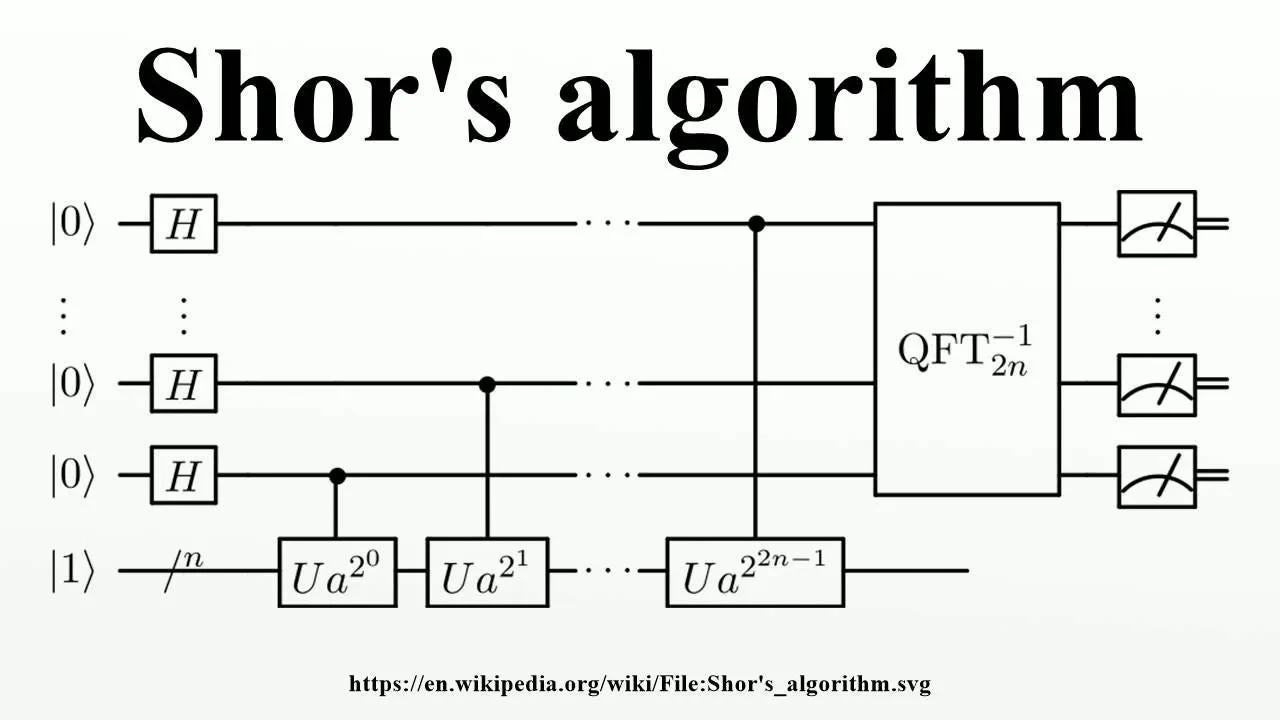
is a quantum algorithm developed by mathematician Peter Shor in 1994, which provides an efficient method for factoring large integers into their prime factors. This problem, known as integer factorization, is at the core of the security of many classical cryptographic systems, such as RSA encryption. RSA relies on the fact that factoring a large composite number (the product of two large primes) is computationally difficult, and thus, secure public-key encryption can be achieved. However, Shor's algorithm has shown that quantum computers can factor large numbers exponentially faster than classical algorithms, posing a potential threat to the security of RSA and similar cryptographic systems.
Shor’s algorithm operates in polynomial time, which contrasts sharply with the best-known classical factoring algorithms that operate in sub-exponential time. The core of the algorithm is based on quantum period-finding, a problem that is solvable much more efficiently with quantum resources. The process involves finding the period of a function associated with the number to be factored, which can then be used to extract factors of the number. Classical computers are unable to perform this task efficiently for large numbers, but Shor's algorithm leverages quantum superposition and quantum parallelism to compute the period much faster than classical methods, providing an exponential speedup.
The importance of Shor’s algorithm lies in its implications for modern cryptography. Quantum computers that can run Shor's algorithm efficiently could break many encryption schemes that are widely used today, including RSA, DSA (Digital Signature Algorithm), and DH (Diffie-Hellman) key exchange protocols. This has led to the development of quantum-resistant cryptographic algorithms and the field of post-quantum cryptography. While large-scale quantum computers capable of running Shor’s algorithm are not yet available, its existence highlights the need for cryptographic systems that are secure against quantum attacks. Researchers are currently working on developing encryption methods that remain secure even in the presence of powerful quantum computers, ensuring that the advent of quantum computing will not compromise the privacy and security of digital communications.
5.Quantum-safe Encryption
Quantum-safe Encryption
refers to cryptographic systems and algorithms designed to be secure against the potential future threats posed by quantum computers. Quantum computers, when fully developed, could break many of the cryptographic techniques that currently protect data, such as RSA, ECC (Elliptic Curve Cryptography), and DSA (Digital Signature Algorithm), by running algorithms like Shor's algorithm, which can efficiently factor large numbers and solve discrete logarithm problems. This poses a significant risk to the confidentiality and integrity of sensitive data, as quantum computers could potentially break the widely used public-key cryptographic systems, rendering them insecure. Quantum-safe encryption, therefore, focuses on developing cryptographic methods that are resistant to quantum computing attacks.
The main goal of quantum-safe encryption is to create algorithms that can withstand quantum computing’s ability to break classical encryption systems. Several approaches are being explored to develop quantum-resistant cryptographic methods, including lattice-based cryptography, hash-based cryptography, code-based cryptography, multivariate polynomial cryptography, and isogeny-based cryptography. These approaches are considered "quantum-safe" because their security is based on mathematical problems that are believed to be hard for quantum computers to solve efficiently. For example, lattice-based cryptography relies on the difficulty of problems like the shortest vector problem and learning with errors, which are not easily solvable by quantum computers.
One of the major efforts to create quantum-safe encryption standards is being led by the National Institute of Standards and Technology (NIST), which initiated a multi-year process to evaluate and standardize post-quantum cryptographic algorithms. In 2022, NIST selected several quantum-safe encryption algorithms for standardization, including schemes based on lattice-based cryptography, such as Kyber for public-key encryption and NTRU for key exchange. These algorithms are being integrated into the existing cryptographic infrastructure to ensure that systems remain secure in the face of quantum computing’s potential capabilities.

6.Lattice-based Cryptography
Lattice-based Cryptography
is a class of cryptographic schemes that rely on the mathematical hardness of lattice problems. Lattices are mathematical structures that consist of a grid of points in multidimensional space, and lattice-based problems involve finding short vectors or solving equations within these grids. The most well-known problems in lattice-based cryptography are the Shortest Vector Problem (SVP) and the Learning With Errors (LWE) problem. These problems are considered hard to solve, even for quantum computers, making lattice-based cryptography a promising candidate for quantum-resistant encryption methods. Unlike classical problems such as integer factorization or discrete logarithms, which quantum computers can solve efficiently using algorithms like Shor's algorithm, lattice-based problems are believed to remain difficult even for quantum algorithms, offering a level of security that is resistant to quantum attacks.
Lattice-based cryptographic schemes are being developed for a variety of cryptographic primitives, including public-key encryption, digital signatures, key exchange, and homomorphic encryption. Some well-known lattice-based encryption schemes include NTRU (used for key exchange) and FrodoKEM (a key exchange algorithm based on the Learning With Errors problem). Lattice-based cryptography is particularly attractive because it offers strong security guarantees and can be used for advanced applications like fully homomorphic encryption (FHE), which allows computations to be performed directly on encrypted data without decrypting it. This makes lattice-based cryptography highly suitable for privacy-preserving computations in cloud computing and secure multi-party computations
One of the main advantages of lattice-based cryptography is its efficiency compared to other quantum-resistant algorithms. While lattice-based schemes often require larger key sizes and more computational resources than traditional public-key systems like RSA or ECC, their security and practicality make them an attractive option for post-quantum cryptography. Additionally, lattice-based schemes have the potential to be implemented efficiently on hardware, and many are already being considered for standardization in post-quantum cryptography by organizations such as the National Institute of Standards and Technology (NIST). NIST has already selected several lattice-based algorithms for further development, including Kyber, a public-key encryption algorithm, and NTRU, a key exchange algorithm, both of which are seen as strong candidates for future quantum-safe cryptographic systems.

7.Quantum Random Number Generation
Quantum Random Number Generation
is a method of generating truly random numbers based on the inherent unpredictability of quantum mechanical processes. Unlike classical random number generators, which rely on algorithms or physical processes that can, in theory, be predicted if enough information is known, QRNG takes advantage of the fundamental randomness of quantum mechanics, specifically the behavior of quantum particles such as photons. This randomness is considered intrinsic because quantum events, like the decay of particles or the measurement of quantum states, cannot be precisely determined ahead of time, making the numbers produced by QRNG fundamentally unpredictable and uncorrelated.
The most common method of QRNG involves measuring quantum phenomena such as the polarization of photons, quantum interference, or quantum fluctuations. For example, one approach uses the polarization of a photon emitted by a quantum source. The photon is passed through a polarizing filter, and the outcome—whether the photon is detected in one of the two possible states (horizontal or vertical)—is used as a random bit. The result of this measurement is entirely random because, according to quantum theory, the state of the photon before measurement is in a superposition, meaning it has no definite value until observed. This guarantees that the outcome is unpredictable and provides a true source of randomness.
QRNG is considered particularly important for cryptographic applications because secure encryption depends on the quality of random numbers used for generating keys, initialization vectors, and other cryptographic elements. Classical pseudo-random number generators (PRNGs) use algorithms to generate numbers that appear random but are deterministic. If an attacker knows the algorithm and the initial conditions (seed), they can predict the sequence of random numbers. However, because QRNG is based on the unpredictable nature of quantum mechanics, it cannot be replicated or predicted, providing a higher level of security in cryptographic systems. This makes QRNG ideal for generating encryption keys, securely transmitting information, and ensuring the integrity of cryptographic protocols like Quantum Key Distribution (QKD).

8.Zero-Knowledge Proofs/h2>
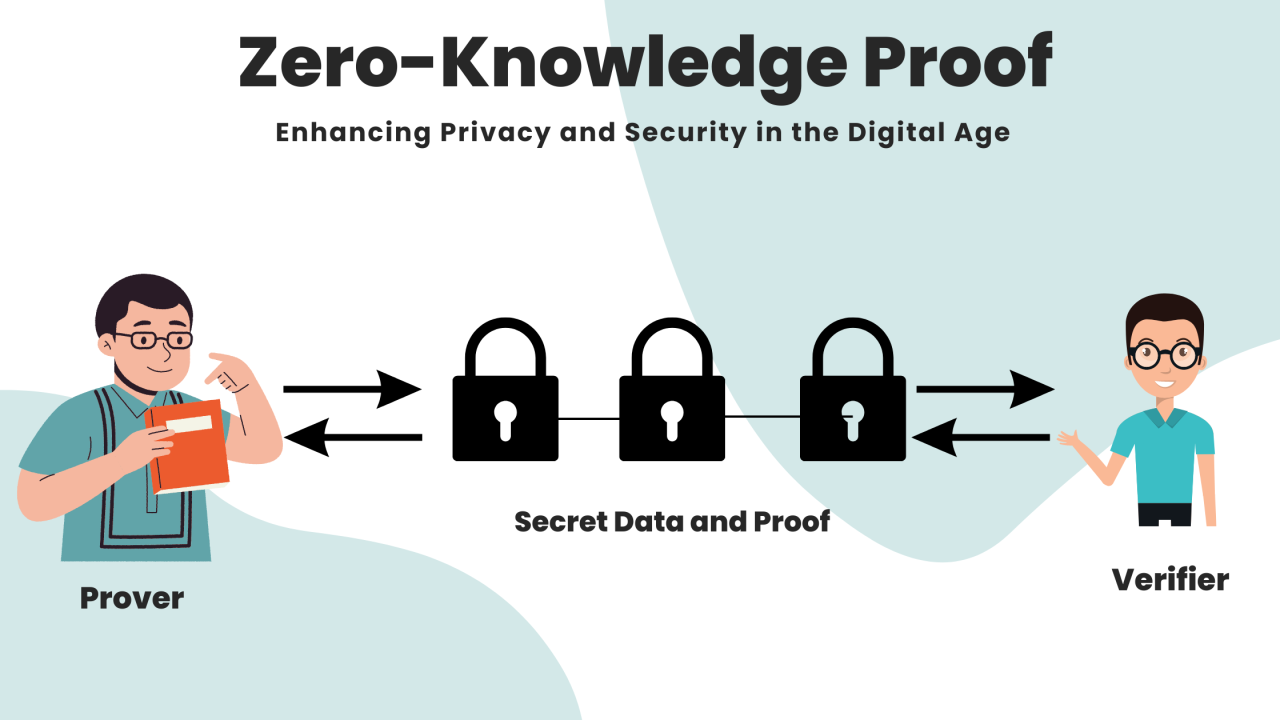
Zero-Knowledge Proofsare cryptographic methods that allow one party (the prover) to prove to another party (the verifier) that they know a piece of information or a secret, without actually revealing the information itself. The primary goal of a zero-knowledge proof is to demonstrate knowledge of a fact while maintaining the privacy of the fact itself. This concept is foundational in areas such as privacy-enhancing technologies, secure authentication systems, and blockchain applications, where users need to prove their identity or the validity of their data without exposing sensitive information.
A classic example of a zero-knowledge proof is the Ali Baba Cave analogy, where the prover wants to convince the verifier that they know the secret to open a locked door inside a cave, without revealing the secret. The prover can walk through a two-path cave and, by repeating the process several times, convince the verifier that they indeed know how to unlock the door without actually showing how it's done. The process relies on the fact that the prover can demonstrate their knowledge without revealing the actual secret.
Zero-knowledge proofs are used extensively in blockchain and cryptocurrencies to enhance privacy and scalability. For instance, in the cryptocurrency Zcash, ZKPs (specifically, zk-SNARKs or Zero-Knowledge Succinct Non-Interactive Arguments of Knowledge) allow transactions to be verified without revealing the transaction amounts, sender, or receiver, providing enhanced privacy for users. This is especially useful in scenarios where confidentiality is paramount but there is still a need for trustless verification. Zero-knowledge proofs can also be used for secure authentication systems, where a user can prove they know a password without actually sending the password to the server, reducing the risk of exposure.
Zero-Knowledge Proofsare cryptographic methods that allow one party (the prover) to prove to another party (the verifier) that they know a piece of information or a secret, without actually revealing the information itself. The primary goal of a zero-knowledge proof is to demonstrate knowledge of a fact while maintaining the privacy of the fact itself. This concept is foundational in areas such as privacy-enhancing technologies, secure authentication systems, and blockchain applications, where users need to prove their identity or the validity of their data without exposing sensitive information.
A classic example of a zero-knowledge proof is the Ali Baba Cave analogy, where the prover wants to convince the verifier that they know the secret to open a locked door inside a cave, without revealing the secret. The prover can walk through a two-path cave and, by repeating the process several times, convince the verifier that they indeed know how to unlock the door without actually showing how it's done. The process relies on the fact that the prover can demonstrate their knowledge without revealing the actual secret.
Zero-knowledge proofs are used extensively in blockchain and cryptocurrencies to enhance privacy and scalability. For instance, in the cryptocurrency Zcash, ZKPs (specifically, zk-SNARKs or Zero-Knowledge Succinct Non-Interactive Arguments of Knowledge) allow transactions to be verified without revealing the transaction amounts, sender, or receiver, providing enhanced privacy for users. This is especially useful in scenarios where confidentiality is paramount but there is still a need for trustless verification. Zero-knowledge proofs can also be used for secure authentication systems, where a user can prove they know a password without actually sending the password to the server, reducing the risk of exposure.

Comments